数学概念集
大数定理
在随机事件的大量重复出现中,往往呈现几乎必然的规律,
均方根误差 rmse
√[∑di^2/n]=Re
式中:n 为测量次数;di 为一组测量值与真值的偏差。又叫标准差是方差的算术平方根标准差能反映一个数据集的离散程度。标准差,是一组数据标准差值,(用了所有数据与平均值的差值,的平方和)的平均,然后开方。
平均绝对百分误差 MAPE

相关系数: corrcoef
相关系数在0~1之间,用来描述两组数据的相关程度,在0是表示不相关,在1时表示最相关.
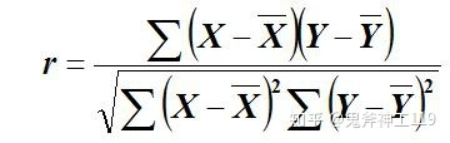
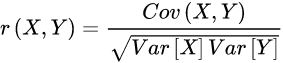
matlab中可以直接调用corrcoef 用法
方差
Σ(xi-

大数定理
在随机事件的大量重复出现中,往往呈现几乎必然的规律,
复角
arg。
复数的幅角也就是在 z = re iθ 中的θ 。z = r*(cosθ + i sinθ);
可以记作:Arg(z)。
求法:z = r*(cosθ + i sinθ),z=a+bi; θ = arctan(b/a);
平移不变性
只是它本身的平移,在平移之后,对于它的某种性质并不发生改变。
联合密度函数?:
最大似然估计
?:P(A|θ),事件 A 发生的概率与某一未知参数θ
有关,对θ在一定范围内取值,找到使 P (A) 也就是 A 发生的概念最大.
泰勒展开式
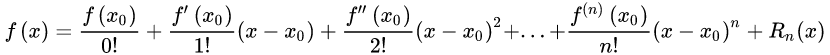
泰勒级数展开, 是在某一点展开的。
常见泰勒级数展开式
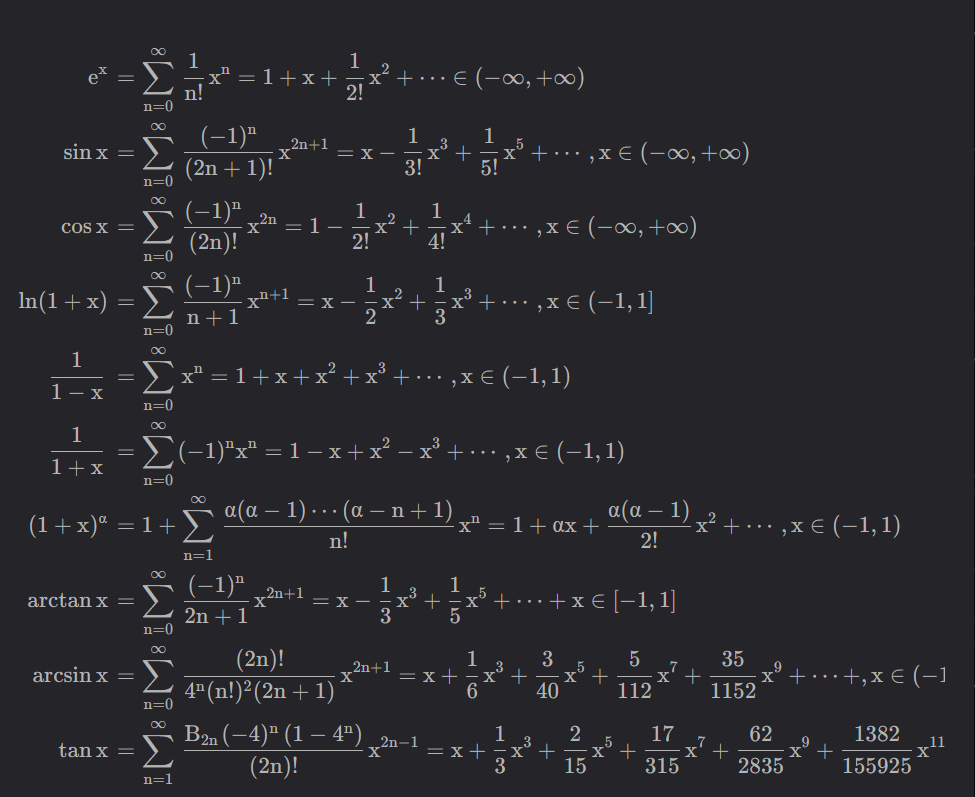
方向导数
对于一元导数的扩展. 方向导数是在函数定义域的内点对某一方向求导得到的导数
导数扩展, 百度百科链接
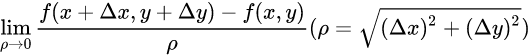
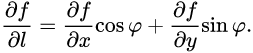
梯度
梯度的本意是一个向量(矢量),表示某一函数在该点处的方向导数沿着该方向取得最大值
百度百科链接
在空间的每一个点都可以确定无限多个方向,一个多元函数在某个点也必然有无限多个方向。因此,导数在这无限多个方向导数中最大的一个(它直接反映了函数在这个点的变化率的数量级)
梯度3
梯度 ∇f (x1, …, xn) 偏导数组成的向量 (df / dx1, …, df / dxn). 若 f (x, y, z) = 3xy + z² 则 ∇f = (3y, 3x, 2z)
梯度-自理解
梯度是一个方向, 一个用单位向量表示的方向。在某一个点其方向导数的值,在某个方向取得最大值的时候,这个方向就是梯度方向,最大值就是梯度的模。
首先来看看方向导数的表达: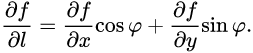
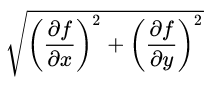
关于梯度的例题
∇哈密顿算子
黑塞矩阵 (Hessian Matrix)
多元函数泰勒级数
Hadamard
Hadamard 乘积,表示对应位置元素相乘。
写错了这个;Hadamard 乘积是元素乘法,但是是*符号,⭕️里面一个点是,kron_rao 积;kron_rao 积就是正确的

Kron_rao
\\192.168.31.2\docker\alist\杨树云文档\论文\文老师\PPT\ESPRIT复习文件\双基地\矩阵的Kronecker积、Khatri-Rao积、Hadamard积-CSDN博客.pdf
[矩阵的Kronecker积、Khatri-Rao积、Hadamard积-CSDN博客.pdf](file:///%5C%5C192.168.31.2/docker/alist/%E6%9D%A8%E6%A0%91%E4%BA%91%E6%96%87%E6%A1%A3/%E8%AE%BA%E6%96%87/%E6%96%87%E8%80%81%E5%B8%88/PPT/ESPRIT%E5%A4%8D%E4%B9%A0%E6%96%87%E4%BB%B6/%E5%8F%8C%E5%9F%BA%E5%9C%B0/%E7%9F%A9%E9%98%B5%E7%9A%84Kronecker%E7%A7%AF%E3%80%81Khatri-Rao%E7%A7%AF%E3%80%81Hadamard%E7%A7%AF-CSDN%E5%8D%9A%E5%AE%A2.pdf)
可以好好看看这个解释
连乘

/
奇异值分解 svd
SVD,,特征值分解,主成分分析PCA,协方差矩阵,矩阵分析
M =
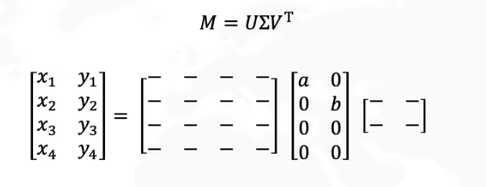
两种线性变换:拉伸与旋转,对角矩阵
两个矩阵都为正交矩阵
SVD分解,后的U 与V都是标准正交矩阵,(
对角矩阵在右(列变换)
对角矩阵在左(行变换)
问题:从变换的角度可以把奇异值分解看做,一种线性变换,旋转,拉伸,再旋转。那么不从变换的角度为什么Σ中越大的就是 越是主成分?
U为按列分块得到的向量 正交,V为按行分块的矩阵 正交
SVD分解相当于分层,每一层都是原始矩阵的大小,而且不同层级正交
不同层相加 u1 * λ1 * v1 + ... + un * λn * vn

求解:
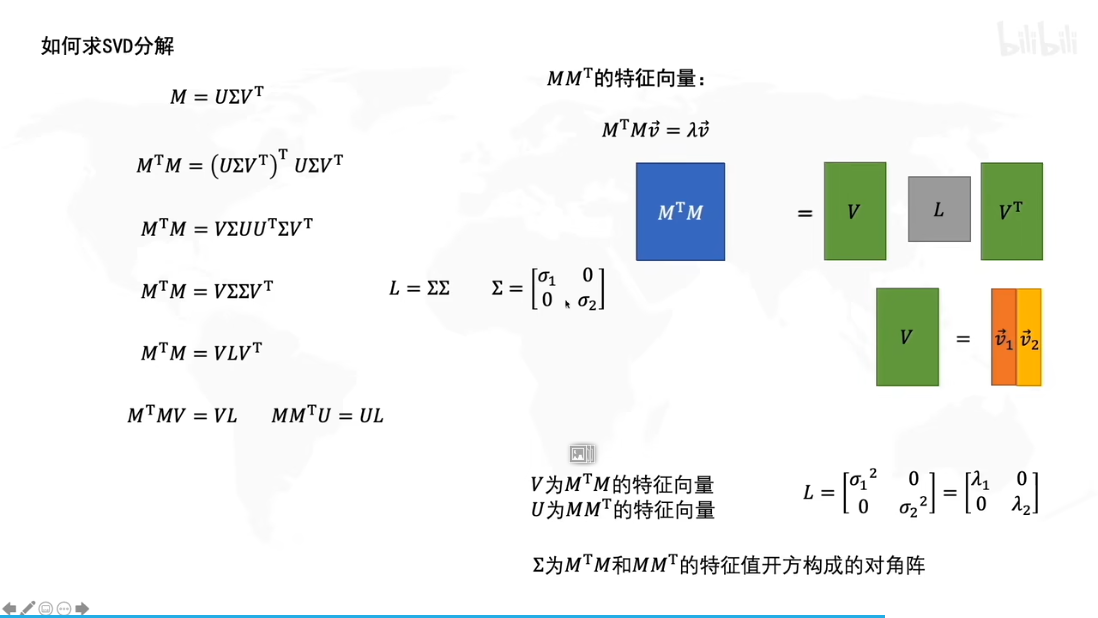
奇异值分解是特征值分解的推广
什么是特征值分解?
特征值分解 Ax = λx,A为方阵
主成分分析 PCA principal Component analysis
PCA大致原理:
- 找数据中心点
- 旋转坐标系,判断最大特征值
- 数据标准化
- 查看 ( 样本不同属性的相关度[二维十字坐标系] ),新属性在整个样本属性中的重要性【占比】
插值
插值, 在数值分析这门分支学科中出现过. 二维平面的插值可以看看这篇博客
反距离插值法
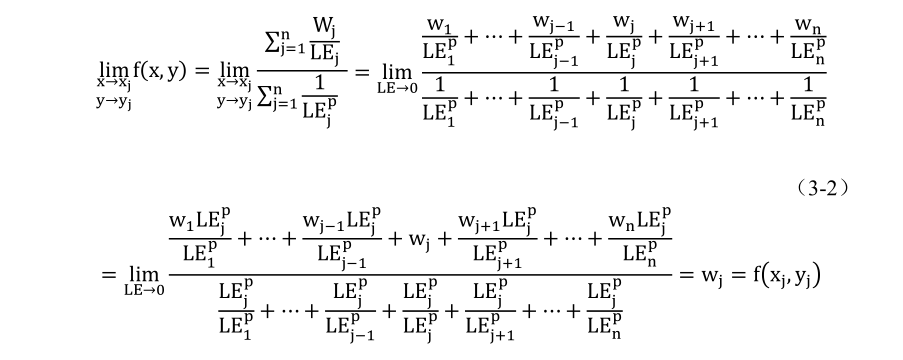
其中

Sech 函数
Sechx=1/chx=2/[e^(x)+e^(-x)]
lipschitz 利普希茨条件

矩阵
- 对称矩阵:对称矩阵(Symmetric Matrices)是指以主对角线(↘)为对称轴,转置等于本身。
- 正定矩阵:
稀疏矩阵和稠密矩阵
- 在矩阵中,若数值为 0 的元素数目远远多于非 0 元素的数目,并且非 0 元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非 0 元素数目占大多数时,则称该矩阵为稠密矩阵
欧拉公式
蒙特卡洛模拟
用随机模拟的方法,干出一个概率出来,只要随机模拟的次数越多,这个概率也就越准。
知道一个总的指标值 Z 是多少,要求指标值 Y 是多少, Y 在 Z 中
有一个约束边界,可以用随机的方法,把粒子放到,对应的指标 Y 里面
然后用大量随机方法把粒子丢到总的 Z 中
Zn Z 中的粒子 Yn y 中的粒子
Yn/Zn * Z = Y
这样就能得到指标值 Y
https://zhuanlan.zhihu.com/p/369099011
如何通俗地理解「蒙特卡洛方法」,它解决问题的基本思路是什么,目前主要应用于哪些领域? - 蛤蟆仙人的回答 - 知乎 https://www.zhihu.com/question/441076840/answer/1870543794
这个也讲的比较详细
期望
其中
例如:

数学期望的理解 - shawnxiang-AI 的文章 - 知乎 https://zhuanlan.zhihu.com/p/357748884
这个讲得比较清晰
张量
一阶张量是一个矢量,二阶张量是一个矩阵,三阶或更高阶的张量叫做高阶张量。
张量的阶数(the order of a tensor)也称为维数(dimensions)、模态(modes)、或方式(ways)。
https://blog.csdn.net/AIMZZY/article/details/106528350
卷积
卷积、旋积或褶积 (英语:Convolution) 是通过两个函数 f 和 g 生成第三个函数的一种数学运算
https://baike.baidu.com/item/卷积/9411006?fr=aladdin
交叉熵
【介绍了交叉熵,从数学的角度】 https://blog.csdn.net/weixin_45665708/article/details/111299919
【代码角度】 https://zhuanlan.zhihu.com/p/35709485
【】 https://zhuanlan.zhihu.com/p/35709485
无偏估计
无偏估计的意义是:在多次重复下,它们的平均数接近所估计的参数真值。无偏估计常被应用于测验分数统计中。
在一些统计学上,除以 n-1, 与除以 n,在小样本情况下 n-1 ,可能会更准一些?
一元二次方程求根
一元二次方程 ax2+bx+c=0 求根
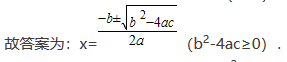

酉矩阵
1
酉矩阵是一个非常重要的数学概念,它在量子力学和通信领域中被广泛应用。简单来说,一个矩阵是酉矩阵,当且仅当它满足以下两个条件:
- 矩阵的转置等于它的逆,即
,其中 表示 的厄米共轭转置, 表示单位矩阵。 - 矩阵的所有列向量(或行向量)都是单位向量,并且两两正交,即
中的每个元素都等于 或 。
这个定义可能有些抽象,下面给出一个简单的例子来说明什么是酉矩阵。
考虑一个二维空间中的旋转操作,可以用一个的矩阵 来表示,其中第一列是旋转后的 轴方向的单位向量,第二列是旋转后的 轴方向的单位向量。例如,下面的矩阵表示一个顺时针旋转 度的操作:
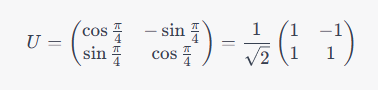
我们可以验证,这个矩阵满足酉矩阵的定义:
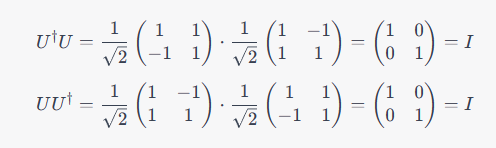
因此,这个矩阵是一个酉矩阵。它代表了一个旋转操作,可以用于各种应用,例如图像处理、量子力学中的门操作等等。
变化率
变化率指的是某个变量随时间的变化速率,通常用导数来表示。具体来说,如果一个变量
这个式子的含义是:当时间
如果变量的变化率是常数,那么它的变化是线性的,可以用直线来表示。如果变化率不是常数,那么它的变化就是非线性的,通常需要用更复杂的函数来表示。
相关系数
相关系数是用于衡量两个变量之间线性关系强度的统计量。它的值介于-1 和 1 之间,当相关系数为正数时,表示两个变量呈正相关;当相关系数为负数时,表示两个变量呈负相关;当相关系数为 0 时,表示两个变量没有线性关系。
在统计学中,通常使用皮尔逊相关系数(Pearson correlation coefficient)来衡量两个变量之间的相关性。它的计算公式如下:
其中,x和y分别是两个变量的观测值,μx和μy分别是两个变量的均值,σx和σy分别是两个变量的标准差,n是观测值的数量。
计算皮尔逊相关系数的具体步骤如下:
- 计算每个变量的均值和标准差;
- 计算每个观测值与对应变量的均值之间的差;
- 将每个差值乘以另一个变量的差值,得到每对观测值的乘积;
- 计算乘积的总和;
- 将总和除以观测值数量n,得到样本的协方差;
- 将协方差除以两个变量的标准差的乘积,得到样本的相关系数。
除了皮尔逊相关系数,还有其他的相关系数,如斯皮尔曼相关系数(Spearman correlation coefficient)和肯德尔相关系数(Kendall correlation coefficient),它们分别用于衡量两个变量之间的等级关系和顺序关系。
复数的导数

https://zhuanlan.zhihu.com/p/108998452
复数矩阵的二范数

特征值分解(evd)与奇异值(svd)分解
奇异值分解(SVD) - 漫漫成长的文章 - 知乎 https://zhuanlan.zhihu.com/p/29846048
特征值分解:


如何求解特征值
Import 资料:
https://www.cnblogs.com/liuhuacai/p/12902144.html 共轭梯度法求解 Ax=b
https://www.cnblogs.com/liuhuacai/p/13019406.html 乘幂法求解 A 最大特征值
https://zhuanlan.zhihu.com/p/305626910 # 计算矩阵特征问题的幂法
https://zhuanlan.zhihu.com/p/305670306 共轭梯度
https://www.bilibili.com/video/BV1zv4y1o7ZX/ # 幂法 b 站视频

Gpt 给出,未验证。

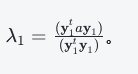
特征值手算:

矩阵 ATA 是否可逆

狄拉克δ函数
在 x 不等于 0 时,y=0。x=0 时,y=1

高斯核函数
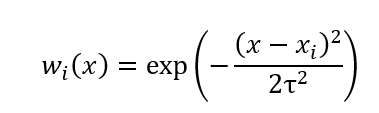
正态分布的函数
反常积分
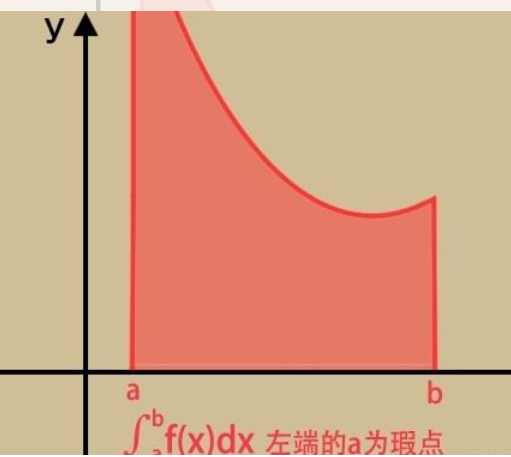
反常积分又叫广义积分,是对普通定积分的推广,指含有无穷上限/下限,或者被积函数含有瑕点的积分,前者称为无穷限广义积分,后者称为瑕积分(又称无界函数的反常积分
如果函数 f (x) 在点 a 的一个邻域内无界,那么点 a 称为函数 f (x) 的瑕点(也称无界间断点)。无界函数的反常积分又称为瑕积分。
伴随矩阵

二次型

维达定理

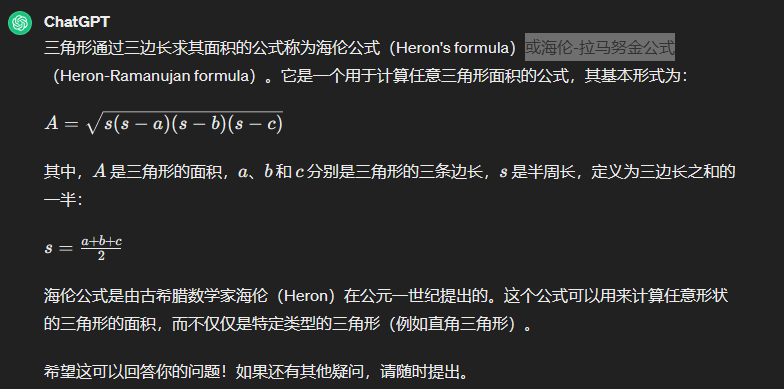
三角形型三边求面积

一元二次方程虚数解

素数
素数(Prime number)是数论中的一个基本概念,指的是满足以下条件的自然数:
- 它大于 1。
- 它没有除了 1 和它本身以外的正因数(也叫约数)。
换句话说,一个素数是一个自然数,它不能被任何其他自然数(除了 1 和它自己)整除。例如,2、3、5、7、11、13、17、19、23 等都是素数。
让我们来详细解释一下这两个条件:
-
大于 1:素数必须大于 1,因为 1 没有除自身以外的因数,但它不被认为是素数,因为它是乘法的单位元素,任何数乘以 1 都等于它本身。
-
没有其他正因数:这意味着除了 1 和它本身之外,没有其他正整数能够整除这个数。例如,数字 6 不是素数,因为它可以被 2 和 3 整除。
素数在数学中有许多重要的性质和应用,例如它们是整数分解的基础,也是现代密码学中公钥加密算法(如 RSA 算法)的数学基础。素数的分布没有简单的公式,但它们在数学上有许多有趣的性质和猜想,如哥德巴赫猜想、孪生素数猜想等。素数的研究是数论中最古老和最活跃的领域之一。
拉格朗日极值法
或者叫拉格朗日数乘法


伪逆
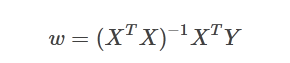

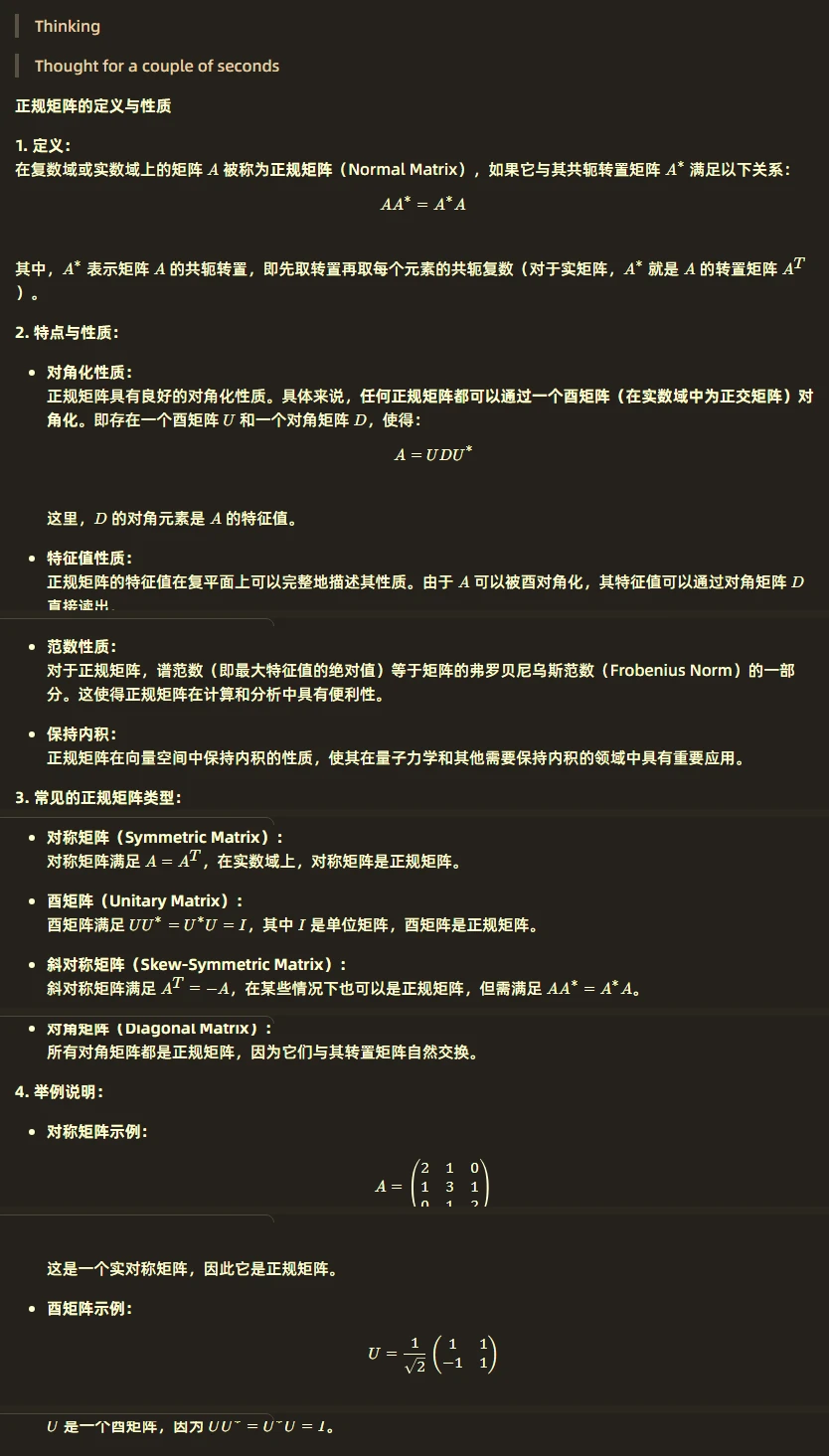
正规矩阵